评价类---决策

层次分析法----定权（相对客观）

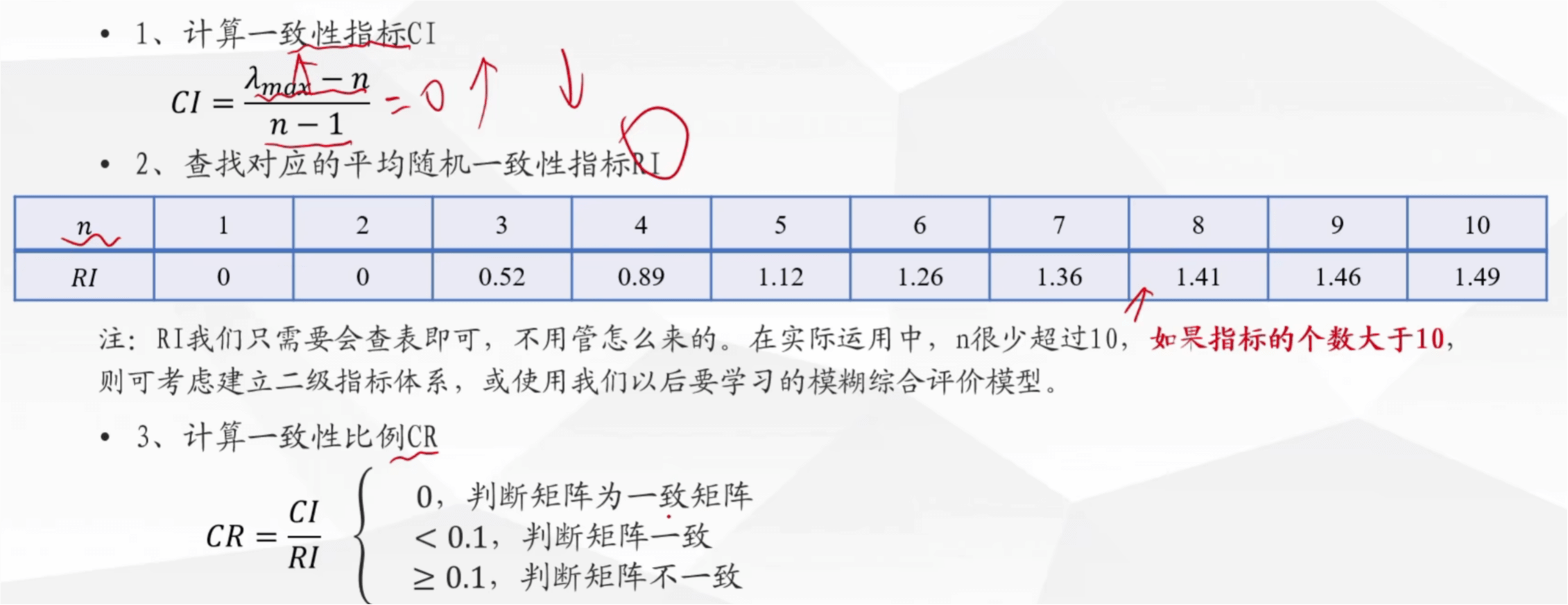
一致矩阵的条件

归一化是指将其加起来，看占的比重

求权重的方法

# 示例
1 1/2      1/(1+2)  (1/2)/(1/2+1)      2/3         1/3
2 1        2/(1+2)   1/(1/2+1)         4/3         2/3

import numpy as np  
  
#定义判断矩阵A  
A = np.array([[1,2,3,5],[1/2,1,1/2,2],[1/3,2,1,2],[1/5,1/2,1/2,1]])  
  
#计算每列的和  
# np.sum 函数可以计算一维数组中所有元素的总和。  
# 还可以通过指定 axis 参数来计算多维数组的某个维度上的元素总和。例如，在二维数组中，axis=0 表示按列计算总和，axis=1 表示按行计算总和  
ASum = np.sum(A,axis=0)  
  
# 获取A的行和列，0 是获取行，类似于 size
n= A.shape[0]  
#归一化，二维数组除以一维数组，会自动将一维数组扩展为与二维数组相同的形状，然后进行逐元素的除法运算。  
stand_A = A / ASum  
#各列相加到同一行  
ASumr = np.sum(stand_A, axis=1)  
# 计算权重向量  
weights = ASumr / n  
print(weights)

# 示例
1 1/2      1/2   sqrt(1/2)  在归一化处理
2 1         2     sqrt(2)

import numpy as np  
  
# 定义判断矩阵A  
A = np.array([[1,2,3,5],[1/2,1,1/2,2],[1/3,2,1,2],[1/5,1/2,1/2,1]])  
  
# 获取A的行和列，0 是获取行，类似于 size 
n = A.shape[0]  
  
# 将A中每一行元素相乘得到一列向量  
# np.prod 函数可以计算一维数组中所有元素的乘积。  
# 还可以通过指定 axis 参数来计算多维数组的某个维度上的元素乘积。例如，在二维数组中，axis=0 表示按列计算乘积，axis=1 表示按行计算乘积。  
prod_A = np.prod(A, axis=1)  
  
# 将新的向量的每个分量开n次方等价求1/n次方  
# np.power 是 NumPy 库中的一个函数，用于对数组中的元素进行幂运算。  
# 例如，可以使用 np.power(a，b)对数组 a 中的每个元素都按照b指数进行运算。  
prod_n_A = np.power(prod_A, 1/n)  
  
# 归一化处理  
re_prod_A = prod_n_A / np.sum(prod_n_A)  
#展示权重结果  
print(re_prod_A)

import numpy as np  
  
#定义判断矩阵A  
A = np.array([[1,2,3,5],[1/2,1,1/2,2],[1/3,2,1,2],[1/5,1/2,1/2,1]])  
#获取A的行和列  
n = A.shape[0]  
#求出特征值和特征向量  
eig_values, eig_vectors = np.linalg.eig(A)  
#找出最大特征值的索引，np.argmax 是 NumPy 库中的一个函数，用于返回数组中最大值的索引  
max_index = np.argmax(eig_values)  
#找出对应的特征向量  
max_vector = eig_vectors[:, max_index]  
# 对特征向量进行归一化处理,得到权重  
weights = max_vector / np.sum(max_vector)  
# 输出权重  
print(weights)

TOPSIS 法

# 假设指标权重都同
import numpy as np  
  
# 从用户输入中接收参评数目和指标数目，并将输入的字符串转换为数值  
print("请输入参评数目:")  
n = int(input()) # 接收参评数目  
print("请输入指标数目:")  
m = int(input()) # 接收指标数目  
  
# 接收用户输入的类型矩阵，该矩阵指示了每个指标的类型(极大型、极小型等)  
print("请输入类型矩阵:1:极大型，2:极小型，3:中间型，4:区间型")  
kind = input().split(" ") #将输入的字符串按空格分割，形成列表  
  
# 接收用户输入的矩阵并转换为numpy数组  
print("请输入矩阵:")  
A = np.zeros(shape=(n, m)) # 初始化一个n行m列的全零矩阵A  
for i in range(n):  
    A[i] = input().split(" ") # 接收每行输入的数据  
    A[i] = list(map(float, A[i])) # 将接收到的字符串列表转换为浮点数列表  
print("输入矩阵为:\n{}".format(A)) # 打印输入的矩阵A  
  
# 极小型指标转化为极大型指标的函数  
def minTomax(maxx, x):  
    x = list(x) # 将输入的指标数据转换为列表  
    ans = [[(maxx - e)] for e in x] #计算最大值与每个指标值的差，并将其放入新列表中  
    return np.array(ans) #将列表转换为numpy数组并返回  
  
# 中间型指标转化为极大型指标的函数  
def midTomax(bestx, x):  
    x = list(x) #将输入的指标数据转换为列表  
    h = [abs(e-bestx)for e in x] # 计算每个指标值与最优值之间的绝对差  
    M = max(h) #找到最大的差值  
    if M == 0:  
        M=1 #防止最大差值为0的情况  
    ans =[[(1-e/M)]for e in h] #计算每个差值占最大差值的比例，并从1中减去，得到新指标值  
    return np.array(ans) #返回处理后的numpy数组  
  
# 区间型指标转化为极大型指标的函数  
def regTomax(lowx,highx ,x):  
    x=list(x) #将输入的指标数据转换为列表  
    M= max(lowx-min(x), max(x)-highx) # 计算指标值超出区间的最大距离  
    if M == 0:  
        M=1 #防止最大距离为0的情况  
    ans =[]  
    for i in range(len(x)):  
        if x[i]<lowx:  
            ans.append([(1-(lowx-x[i])/M)]) # 如果指标值小于下限，计算其与下限距离比例  
        elif x[i]>highx:  
            ans.append([(1-(x[i]-highx)/M)]) #如果指标值大于上限，计算其与上限距离比例  
        else:  
            ans.append([1])#如果指标值在区间内，则直接取为1  
    return np.array(ans) #返回处理后的numpy数组  
  
  
# 统一指标类型，将所有指标转化为极大型指标  
X = np.zeros(shape=(n, 1))  
for i in range(m):  
    if kind[i] == "1": #如果当前指标为极大型，则直接使用原值  
        v = np.array(A[:, i])   # numpy中，这个表示从A中提取第i列  
    elif kind[i] == "2": #如果当前指标为极小型，调用minTomax函数转换  
        maxA = max(A[:, i])  
        v = minTomax(maxA, A[:, i])  
    elif kind[i] == "3": #如果当前指标为中间型，调用midTomax函数转换  
        print("类型三:请输入最优值:")  
        bestA = eval(input())  # 可以接受int和float  
        v = midTomax(bestA, A[:, i])  
    elif kind[i] == "4": #如果当前指标为区间型，调用regTomax函数转换  
        print("类型四:请输入区间[a，b]值a:")  
        lowA = eval(input())  
        print("类型四:请输入区间[a，b]值b:")  
        highA = eval(input())  
        v = regTomax(lowA, highA, A[:, i])  
    if i == 0:  
        X = v.reshape(-1,1)  # 如果是第一个指标，直接替换X数组  
    else:  
        X = np.hstack([X, v.reshape(-1,1)])  # 如果不是第一个指标，则将新指标列拼接到X数组上  
print("统一指标后矩阵为:\n{}".format(X))  # 打印处理后的矩阵X  
  
# 对统一指标后的矩阵X进行标准化处理  
X = X.astype('float')  # 确保X矩阵的数据类型为浮点数  
for j in range(m):  
    X[:,j] = X[:,j] / np.sqrt(sum(X[:,j] ** 2))  # 对每一列数据进行归一化处理，即除以该列的欧几里得范数  
print("标准化矩阵为:\n{}".format(X))  # 打印标准化后的矩阵X  
  
# 最大值最小值距离的计算  
# 计算标准化矩阵每列的最大值  
x_max = np.max(X, axis=0)  
x_min = np.min(X, axis=0)  # 计算标准化矩阵每列的最小值  
d_z = np.sqrt(np.sum(np.square((X - np.tile(x_max,(n, 1))))), axis=1)  
d_f = np.sqrt(np.sum(np.square((X - np.tile(x_min,(n, 1))))), axis=1)  
  
# 计算每个参评对象与最劣情况的距离d-  
print('每个指标的最大值:', x_max)  
print('每个指标的最小值:', x_min)  
  
print('d+向量:', d_z)  
print('d-向量:', d_f)  
#计算每个参评对象的得分排名  
s = d_f / (d_z + d_f)  # 根据d+和d-计算得分s，其中s接近于1则表示较优，接近于0则表示较劣  
Score = 100 * s / sum(s) # 将得分s转换为百分制，便于比较  
for i in range(len(Score)):  
    print(f"第{i+1}个标准化后百分制得分为:{Score[i]}") # 打印每个参评对象的得分

熵权法

原理：计算熵值，熵值越小，离散程度越大，对其影响大，权重越大

import numpy as np # 导入numpy库，并简称为np  
  
# 定义一个自定义的对数函数mylog，用于处理输入数组中的零元素  
def mylog(p):  
    n = len(p) # 获取输入向量p的长度  
    lnp = np.zeros(n) # 创建一个长度为n，元素都为0的新效组lnp  
    for i in range(n): # 对向量p的每一个元素进行循环  
        if p[i] == 0: # 如果当前元素的值为0  
            lnp[i] = 0 # 则在lnp中对应位置也设置为0，因为log(0)是未定义的，这里我们规定为0  
        else:  
            lnp[i] = np.log(p[i]) # 如果p[i]不为0，则计算其自然对数并赋值给lnp的对应位置  
    return lnp # 返回计算后的对数效组  
  
# 定义一个指标矩阵X  
X = np.array([[9, 0, 0, 0],[8, 3, 0.9, 0.5],[6, 7, 0.2, 1]])  
  
# 对矩阵X进行标准化处理，得到标准化矩阵Z  
Z = X / np.sqrt(np.sum(X*X, axis=0))  
print("标准化矩阵 Z=")  
print(Z) #打印标准化矩阵Z  
  
# 计算熵权所霉的变量和矩阵初始化  
n, m = Z.shape # 获取标准化矩阵Z的行数和列数  
# 初始化一个长度为m的数组D，用于保存每个指标的信息效用值  
D = np.zeros(m)  
  
# 计算每个指标的信息效用值  
for i in range(m): # 历Z的每一列  
    x = Z[:, i] # 获取Z的第i列，即第i个指标的所有数据  
    p = x / np.sum(x) # 对第i个指标的数据进行归一化处理，得到概率分布p  
    # 使用自定义的mylog函数计算p的对数。需要注意的是，如果p中含有0，直接使用np.log会得到-inf，这里使用自定义函数避免这个问题  
    e = -np.sum(p * mylog(p)) / np.log(n) # 根据熵的定义计算第i个指标的信息熵e  
    D[i] = 1 - e #根据信息效用值的定义计算D[i]  
  
# 根据信息效用值计算各指标的权重  
W = D / np.sum(D)  # 将信息效用值D归一化，得到各指标的权重W  
print("杈重 W=")  
print(W) # 打印得到的权重数组W

模糊法

基本步骤

• 首先确定因素集（指标）：志愿服务，智育成绩，综合成绩
• 然后确定评语集：优，良好，中等，差
• 确定权重集：可以由专家评价，也可以计算权重的方法计算，得到集合 A
• 确定模糊综合判断矩阵
• 对于上述的模糊判断矩阵求法
  • 找群众打分
  • 由函数求得
• 进行矩阵合成运算：B = A . R
• 然后找矩阵 B 中的最大值，就选它

隶属函数：将指标的值映射到【0，1】，隶属度越大，属于这个集合的程度越大

灰色关联分析法

灰色关联评价的基本步骤：

• 对数据进行正向化处理

• 对数据预处理：每个指标的元素除以该指标元素的平均值，得到一个新矩阵，这个矩阵使用 Z_ij 表示

• 构造母序列：每个对象各个指标中的最大值，用 Y 表示，是一个列向量

• 找到两极最小值和两极最大值

  • 最小值为例：当前指标的一列中，各个对象的指标值减去母序列的值，去绝对值最小的一个数，这是一部分，然后各个指标都如此操作，找到最小值，取这些最小值中的最小值即为两极最小值
  • 两极最小值记为 a，两极最大值记为 b

• 在带入公式 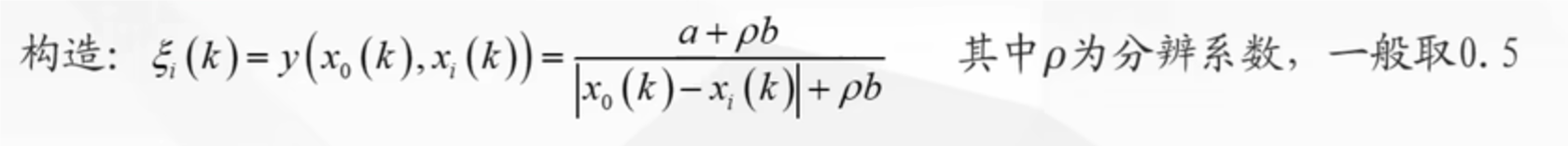计算这个值，得到矩阵（这里面的 x₀ 是母序列，x_i(k)是子序列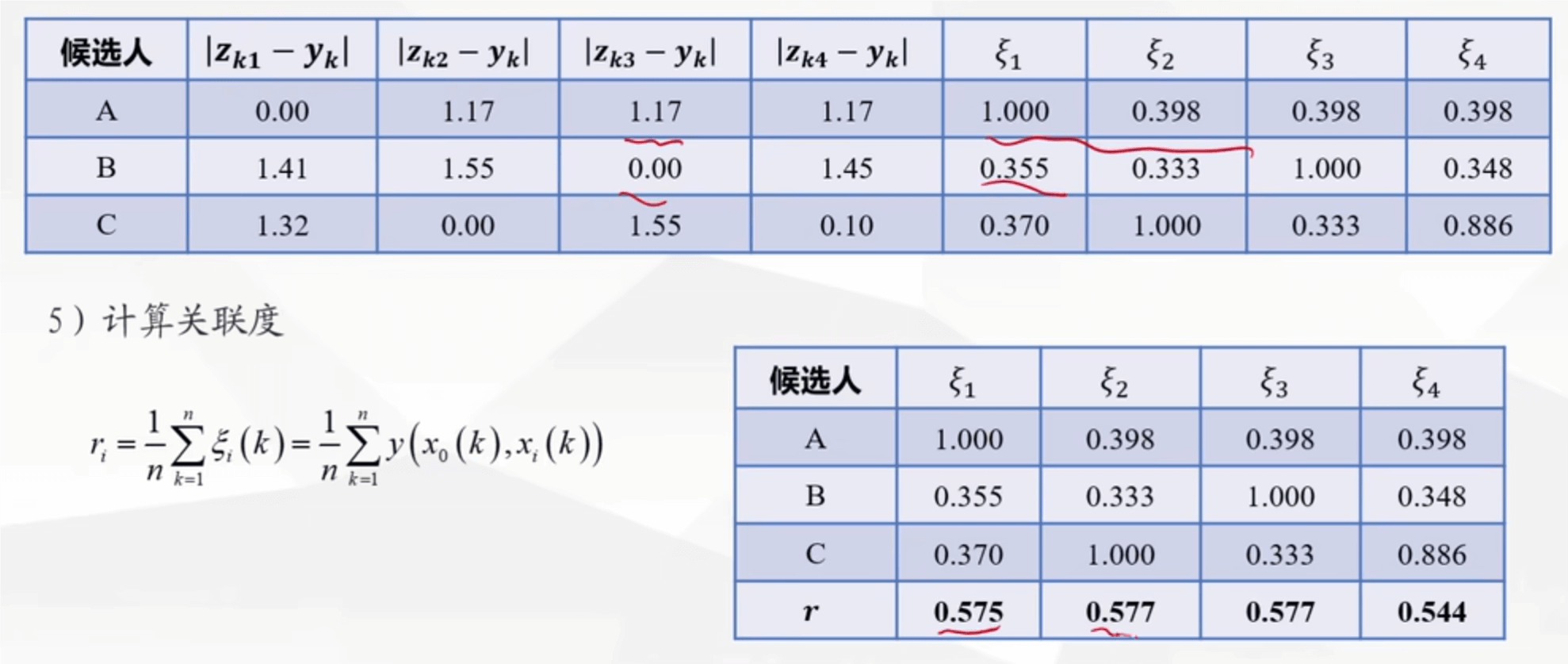

• 

• 

• 计算得分并归一化

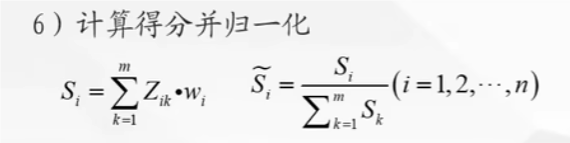
# 灰色关联分析代码
import numpy as np  
  
A = np.array([[55,24,10], [65,38,22], [75,40,18], [100,50,20]])  
# 求出每一列的均值以供后续的数据预处理  
Mean = np.mean(A, axis=0)  
  
# 预处理后的矩阵  
A_norm = A/ Mean  
print('预处理后的矩阵为: ')  
print(A_norm)  
  
# 母序列  
Y = A_norm[:, 0]  
# 子序列  
X = A_norm[: 1:]  
# 计算|X0-Xi|矩阵(在这里我们把X0定义为了Y(母序列))  
absX0_Xi = np.abs(X - np.tile(Y.reshape(-1,1), (1,X.shape[1])))  
# 计算两级最小差a  
a = np.min(absX0_Xi)  
# 计算两级最大差b  
b = np.max(absX0_Xi)  
  
# 分辨系数取0.5  
rho = 0.5  
# 计算子序列中各个指标与母序列的关联系数  
gamma = (a + rho * b)/(absX0_Xi + rho * b)  
print('子序列中各个指标的灰色关联度分别为: ')  
print(np.mean(gamma,axis=0))

主成分分析

这个模型主要是用来降维的，就是把多的变量替换成几个精简的变量，这些变量都能概括出原有变量的意义

使用主成分分析，找出的主成分，要考虑自己能否解释清楚这些主成分，因为看到数据不一定好解释

基本步骤：

• 对原始的样本矩阵进行标准化处理

• 

• 计算特征值和特征向量，注意计算出的特征向量排序后，在带入特征值求出特征向量，这是一 一对应的，即 a₁ 是最大特征值所得出的特征向量

• 

  • 这个是指当前主成分所携带携带原有数据的信息量多少

• 

• 按照主成分的组成，各个指标所占的比重，即 a_1i , a_2i，推断出此时的成分的新的意义，解释出含义，这往往是最难的

import pandas as pd  
import numpy as np  
from scipy import linalg  
  
# 读取Excel文件，从 C 列开始读取  
df = pd.read_excel('filename.xlsx', usecols='C:G')  
  
# df.to_numpy 是 pandas 中 DataFrame 对象的一个方法，用于将 DataFrame 的数据转换为 NumPy 数组  
x = df.to_numpy()  
print(x)  
  
# 标准化数据，mean 求平均值，std 求标准差  
X = (x - np.mean(x,axis=0)) / np.std(x, ddof=1, axis=0)  
# 计算协方差矩阵  
R = np.cov(X.T)  
# 计算特征值和特征向量  
eigenvalues, eigenvectors = linalg.eigh(R)  
# 将特征值数组按降序排列  
eigenvalues = eigenvalues[::-1]  
# 将特征向量矩阵的列按降序排列  
eigenvectors = eigenvectors[:, ::-1]  
# 计算主成分贡献率和累积贡献率  
contribution_rate = eigenvalues / sum(eigenvalues)  
# np.cumsum 是 NumPy 库中的一个函数，用于计算数组元素的累积和。  
cum_contribution_rate =np.cumsum(contribution_rate)  
  
# 打印结果  
print('特征值为: ')  
print(eigenvalues)  
print('贡献率为: ')  
print(contribution_rate)  
print('累计贡献率为: ')  
print(cum_contribution_rate)  
print('与特征值对应的特征向量矩阵为: ')  
print(eigenvectors)

运筹优化类

线性规划

基本步骤：

• 将题目转换为代数形式

• 找出目标函数，决策变量，上述目标函数就是 maxz，决策变量用 s.t 表示，注意一些隐含的约束条件，比如 x>=0

• 注意约束条件的每一个表达式，如果 x 对应的系数为 0，也要写出 0

• 如果题目转换后有两个目标函数，就将其想办法能不能转换为单一目标函数进行，一般是找关系，比如其中一个目标是让风险尽可能小，那么假设最大的一个风险是多少，将这个目标函数转换为约束条件，然后可以枚举风险到当前假设的最大风险，看情况如何，风险对应的收益

==注意：这个适用于小数的计算，整数规划问题不适用==

解释：

• 上述的代数形式都需要转换为矩阵形式，c 就是变量 x 前面的序数组成的矩阵
• 这个约束条件必须是小于等于，不是的话需要转换，如加负号，然后这个函数是求最小值，求最大值，加负号转换目标函数

例子：

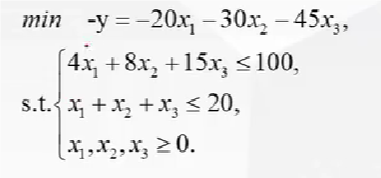
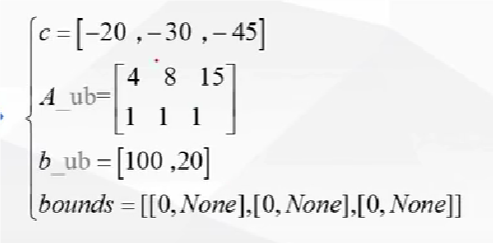
示例：一个有多目标函数的实现代码

# 导入必要的库  
import matplotlib.pyplot as plt # 用于绘图  
from numpy import ones, diag, c_, zeros # 用于创建和操作数组  
from scipy.optimize import linprog # 用于执行线性规划  
  
# 设置matplotlib的参数使其支持LaTeX文本和字体大小  
plt.rc('text', usetex=True)  
plt.rc('font', size=16)  
  
# 线性规划问题的目标函数系数  
c = [-0.05, -0.27, -0.19, -0.185, -0.185]  
# 线性不等式约束的系数矩阵(A*x<=b)  
# 使用c_ 来合并数组，zeros创建一个全0的数组作为第一列，  
# diag创建一个对角阵  
# 这是一个优化，也可以手敲  
A = c_[zeros(4), diag([0.025,0.015,0.055,0.026])]  
# 线性等式约束的系数矩阵和右侧的值(Aeg*x=beq)  
Aeq = [[1, 1.01, 1.02, 1.045, 1.065]]  
beq = [1]  
# 初始化参数a，以及两个用于存储结果的空列表  
a = 0  
aa =[]  
ss =[]  
# 循环，a的值从0开始，以0.001的步长增加，直到0.05  
while a < 0.05:  
    # 创建线性不等式约束的右侧值(b)  
    b = ones(4) * a  
    # 执行线性规划，得到最优解  
    res = linprog(c,A,b,Aeq,beq,bounds=[(0,None),(0,None),(0,None),(0,None),(0,None)])  
    # 提取线性规划的解向量x和最优值0  
    x = res.x  
    Q = -res.fun  
    # 将当前的a值和对应的最优值Q存入列表  
    aa.append(a)  
    ss.append (Q)  
    # a增加0.001  
    a = a + 0.001  
  
# 绘制结果，a值与最优值Q之间的关系图  
plt.plot(aa, ss, 'r*') # 使用红色星号标记数据点  
# 设置坐标轴标签，其中a和Q将使用LaTeX格式显示  
plt.xlabel('$a$')  
plt.ylabel('$Q$',rotation=90)  
# 显示图形  
plt.show()

结果：

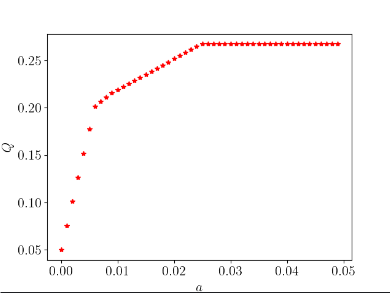
非线性规划

和线性规划类似的思路，函数不同

import scipy
res = scipy.optimize.minimize (fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)

参数解释：

• fun：目标函数: fun (x, * args) x 是形状为 (n, ) 的一维数组 (n 是自变量的数量)
• x0：初值，形状 (n，) 的 ndarray
• method：求解器的类型。如果未给出，有约束时则选择 SLSQP 。
• constraints：求解器 SLSQP 的约束被定义为字典的列表，字典用到的字段主要有：
  • 'type'： str：约束类型："eq" 表示等式，"ineq" 表示不等式 (SLSQP 的不等式约束是 f( x ) ≥ 0 形式
  • 'fun'：可调用的函数或匿名函数：定义约束的函数
• bounds: 变量界限

例子：

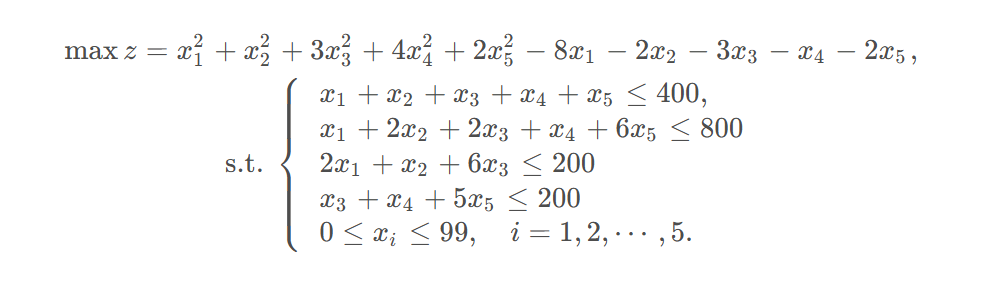
from scipy.optimize import minimize  
import numpy as np  
c1 = np.array([1,1,3,4,2])  
c2 = np.array([-8,-2,-3,-1,-2])  
  
A = np.array([[1,1,1,1,1],[1,2,2,1,6],  
            [2,1,6,0,0],[0,0,1,1,5]])  
b = np.array([400,800,200,200])  
  
# 只能求最小值，所以加了负号  
# np.dot()向量点乘或矩阵乘法  
obj = lambda x: np.dot(-c1,x**2) + np.dot(-c2, x)  
cons = {'type': 'ineq','fun': lambda x: b - A@x } # 约束 b-A*x>=0
bd = [(0,99) for i in range(A.shape[1])]  
  
# res=minimize(obj,np.ones(5)*90,constraints=cons,bounds=bd)  
res = minimize(obj,np.ones(5),constraints=cons,bounds=bd)  
print(res.fun)   
print(res.success)   
print(res.x)

多目标规划

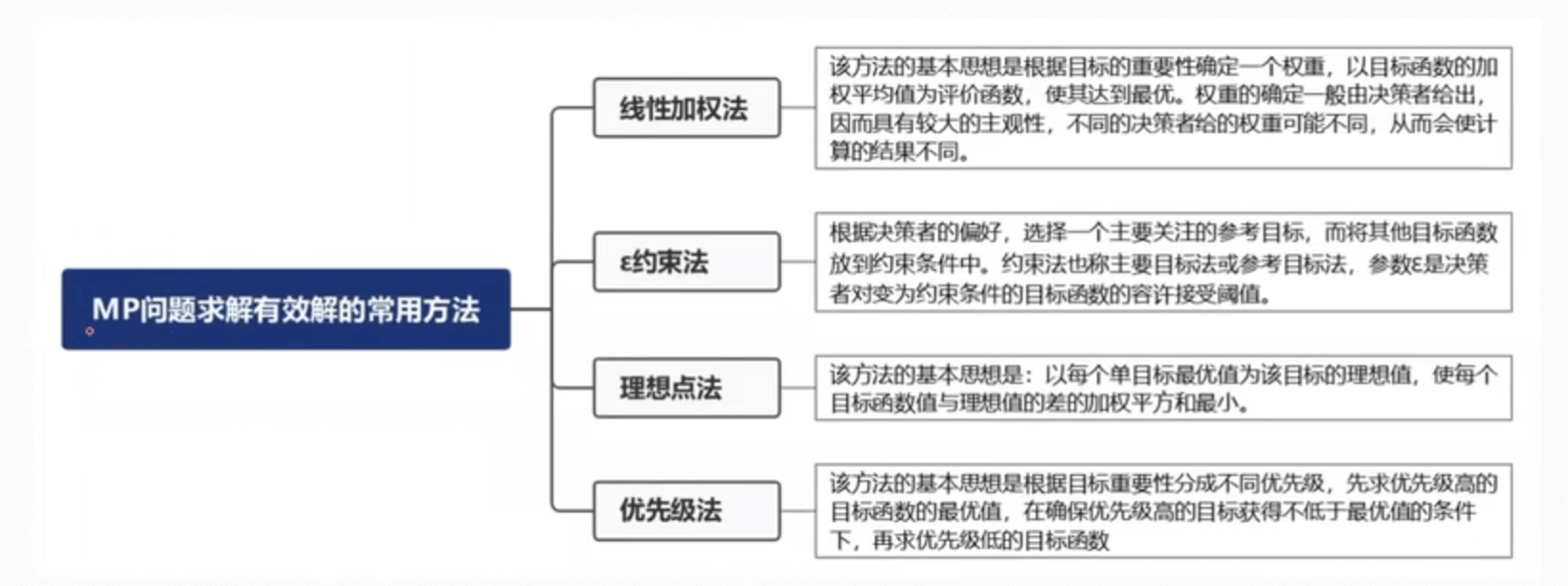
==其中，那个约束法就是线性规划中化解为单目标函数的方法==

注意：

• f_i 权重一般是由专家或者其他方式所得
• 要将多个目标函数统一为最大化和最小化问题 (不同的加 “ - ” 号)才可以进行加权组合
• 如果目标函数量纲不同，则需要对其进行标准化再进行加权，标准化的方法一般是目标函数除以某一个常量，该常量是这个目标函数的某个取值，具体取何值可根据经验确定
• 这个常量有可能题目中会告诉一个参考值
• 对多目标函数进行加权求和是，权重一般由该领域专家给定，实际比赛中，若无特殊说明，我们可令权重相同

例子：

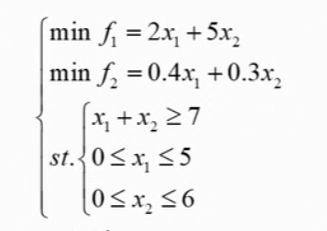
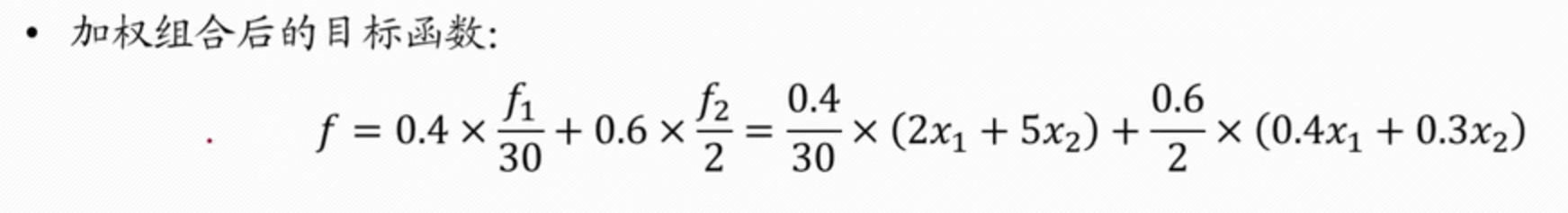
• 上述假设的 f1 的权重为 0.4，f2 的权重为 0.6，参考值 f1 的值为 30 万元，f2 为 2 吨
• 所以这就是合并后的量纲不同
• 转换好了，就用上述线性规划的函数求解

一般数模问题可以进行敏感度分析：就是变化变量值，看结果的差异性比较，进行分析问题 比如这里的权重，变化之后，看结果有何不同，进行分析

启发式算法

模拟退火

示例：解决旅行商问题（TSP 问题）

• 初始化解：随机生成一个初始路径，表示旅行商依次访问城市的顺序。
• 设定初始温度：初始时，系统的 “温度” 很高，容许接受较差的解。初始温度的选择对算法的性能有影响，通常由问题的特性和经验决定。
• 迭代过程：在当前解的基础上进行微小的扰动，例如交换两个城市的顺序，得到一个新的解。计算新解的路径长度与当前解的路径长度之差（ΔE）。如果 ΔE 小于 0，即新解更优，直接接受新解。如果 ΔE 大于 0，以一定的概率（由温度和 ΔE 决定）接受新解。温度高时，概率较大，有较大可能性接受劣解；随着迭代进行，温度逐渐降低，接受劣解的概率减小，算法越来越趋向于选择更好的解。
• 降低温度：在每个迭代步骤后，通过一个降温策略减小温度。典型的降温策略是乘以一个小于 1 的因子。
• 终止条件：当温度降低到足够低（接近零）或者达到最大迭代次数时停止算法。此时，当前解即为所求解。

copy博主代码：模拟退火算法解决TSP问题+Python实现_天池技术圈-阿里云天池 (aliyun.com)

import numpy as np  
import matplotlib.pyplot as plt  
import pdb  
  
"旅行商问题 ( TSP , Traveling Salesman Problem )"coordinates = np.array([[565.0, 575.0], [25.0, 185.0], [345.0, 750.0], [945.0, 685.0], [845.0, 655.0],  
                        [880.0, 660.0], [25.0, 230.0], [525.0, 1000.0], [580.0, 1175.0], [650.0, 1130.0],  
                        [1605.0, 620.0], [1220.0, 580.0], [1465.0, 200.0], [1530.0, 5.0], [845.0, 680.0],  
                        [725.0, 370.0], [145.0, 665.0], [415.0, 635.0], [510.0, 875.0], [560.0, 365.0],  
                        [300.0, 465.0], [520.0, 585.0], [480.0, 415.0], [835.0, 625.0], [975.0, 580.0],  
                        [1215.0, 245.0], [1320.0, 315.0], [1250.0, 400.0], [660.0, 180.0], [410.0, 250.0],  
                        [420.0, 555.0], [575.0, 665.0], [1150.0, 1160.0], [700.0, 580.0], [685.0, 595.0],  
                        [685.0, 610.0], [770.0, 610.0], [795.0, 645.0], [720.0, 635.0], [760.0, 650.0],  
                        [475.0, 960.0], [95.0, 260.0], [875.0, 920.0], [700.0, 500.0], [555.0, 815.0],  
                        [830.0, 485.0], [1170.0, 65.0], [830.0, 610.0], [605.0, 625.0], [595.0, 360.0],  
                        [1340.0, 725.0], [1740.0, 245.0]])  
  
  
# 得到距离矩阵的函数  
def getdistmat(coordinates):  
    num = coordinates.shape[0]  # 52个坐标点  
    distmat = np.zeros((52, 52))  # 52X52距离矩阵  
    for i in range(num):  
        for j in range(i, num):  
            distmat[i][j] = distmat[j][i] = np.linalg.norm(coordinates[i] - coordinates[j])  
    return distmat  
  
# 初始化参数  
def initpara():  
    alpha = 0.99  # 温度下降的比例系数  
    t = (1, 100)  # 温度范围  
    markovlen = 1000  # 每个温度的迭代次数  
  
    return alpha, t, markovlen  
  
  
num = coordinates.shape[0]  # 获取城市的数量，这里是52个  
distmat = getdistmat(coordinates)  # 计算并获取距离矩阵  
  
solutionnew = np.arange(num)  # 初始化一个解，初始解是城市顺序的数组 [0, 1, 2, ..., 51]
solutioncurrent = solutionnew.copy()  # 当前解，初始为初始解，创建副本  
valuecurrent = 99000  # 当前解的初始值，设为一个较大的值（用来比较，实际应为路径总距离）  
  
solutionbest = solutionnew.copy()  # 最优解，初始为初始解  
valuebest = 99000  # 最优解的初始值，设为一个较大的值  
  
alpha, t2, markovlen = initpara()  # 初始化参数，alpha为退火系数，t2为温度范围，markovlen为每个温度下的迭代次数  
t = t2[1]  # 初始温度  
  
result = []  # 用于记录迭代过程中最优解的路径总距离  
  
while t > t2[0]:  # 当温度高于最低温度时继续退火过程  
    for i in np.arange(markovlen):  # 在每个温度下进行一定次数的马尔可夫链长度迭代  
        # 产生新解的方法：两种扰动方式，交换两个城市或三交换  
        if np.random.rand() > 0.5:  # 随机选择一种扰动方式  
            while True:  # 交换两个城市的位置  
                # 生成1~num的随机整数，但是要不同，然后推出循环  
                loc1 = int(np.ceil(np.random.rand() * (num - 1)))  
                loc2 = int(np.ceil(np.random.rand() * (num - 1)))  
                if loc1 != loc2:  
                    break  
            solutionnew[loc1], solutionnew[loc2] = solutionnew[loc2], solutionnew[loc1]  
        else:  # 三交换  
            while True:  
                loc1 = int(np.ceil(np.random.rand() * (num - 1)))  
                loc2 = int(np.ceil(np.random.rand() * (num - 1)))  
                loc3 = int(np.ceil(np.random.rand() * (num - 1)))  
                if ((loc1 != loc2) & (loc2 != loc3) & (loc1 != loc3)):  
                    break  
            # 使loc1 < loc2 < loc3  
            if loc1 > loc2:  
                loc1, loc2 = loc2, loc1  
            if loc2 > loc3:  
                loc2, loc3 = loc3, loc2  
            if loc1 > loc2:  
                loc1, loc2 = loc2, loc1  
            # 将[loc1, loc2)区间的数据插入到loc3之后  
            tmplist = solutionnew[loc1:loc2].copy()  
            solutionnew[loc1:loc3 - loc2 + 1 + loc1] = solutionnew[loc2:loc3 + 1].copy()  
            solutionnew[loc3 - loc2 + 1 + loc1:loc3 + 1] = tmplist.copy()  
  
  
        valuenew = 0  
        for i in range(num - 1):  
            valuenew += distmat[solutionnew[i]][solutionnew[i + 1]]  
        valuenew += distmat[solutionnew[0]][solutionnew[51]]  
        # print (valuenew)  
        if valuenew < valuecurrent:  # 接受该解  
            # 更新solutioncurrent 和solutionbest  
            valuecurrent = valuenew  
            solutioncurrent = solutionnew.copy()  
  
            if valuenew < valuebest:  
                valuebest = valuenew  
                solutionbest = solutionnew.copy()  
        else:  # 按一定的概率接受该解  
            if np.random.rand() < np.exp(-(valuenew - valuecurrent) / t):  
                valuecurrent = valuenew  
                solutioncurrent = solutionnew.copy()  
            else:  
                solutionnew = solutioncurrent.copy()  
    t = alpha * t  
    result.append(valuebest)  
    print(t)  # 程序运行时间较长，打印t来监视程序进展速度  
  
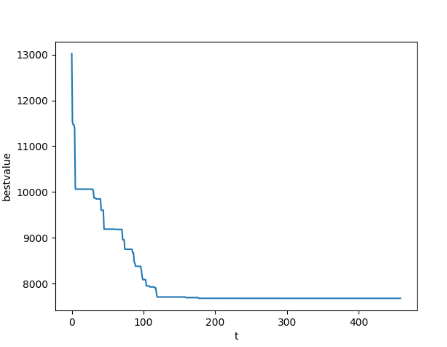
# 用来显示结果  
plt.plot(np.array(result))  
plt.ylabel("bestvalue")  
plt.xlabel("t")  
plt.show()

预测类

线性回归

直线方程参数求解

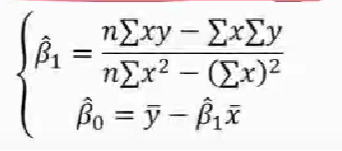
y = β0 + β1x₁ + e e 是误差，属于正态分布，E(e) = 0

检验

回归直线拟合优度

• 回归直线与各观测点的接近程度称为回归直线对数据的拟合优度

• 总平方和可以分解为回归平方和、残差平方和两部分：TSS = ESS + RSS

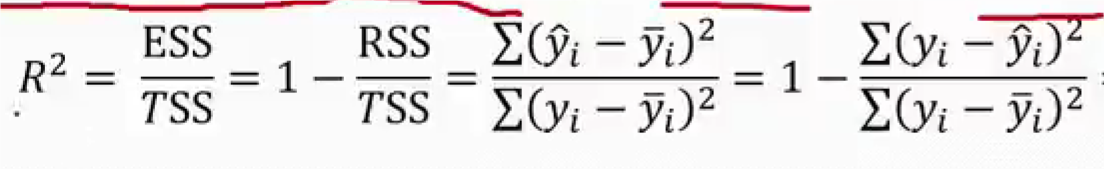
• R² = 0：说明 y 的变化与 x 无关，x 完全无助于解释 y 的变差
• R² = 1：说明残差平方和为 0，拟合是完全的，y 的变化只与 x 有关

==显著性检验==

• 显著性检验的主要目的是根据所建立的估计方程用自变量 x 来估计或预测因变量 v 的取值，当建立了估计方程后，还不能马上进行估计或预测，因为该估计方程是根锯样本数据得到的，它是否真实的反映了变量 x 和 y 之间的关系，则需要通过检验后才能证实

线性关系检验

• 线性关系检验是检验自变量 X 和因变量 Y 之间的线性关系是否显著，或者说，它们之间能否用一个线性模型来表示
• 将均方回归（MSR）与均方残差（MSE）加以比较，应用 F 检验来分析二者之间的差别是否显著
  • 均方回归（MSR）：回归平方和 EES 除以相应的回归自由度（自变量的个数 k）
  • 均方残差（MSE）：残差平方和 RRS 除以相应的残差自由度（n-k-1）
• H₀ (原假设)：β1=0，回归系数与 0 无显著差异，y 与 x 的线性关系不显著
• H₁：β1≠0，回归显著，认为 y 与 x 存在线性关系，所求的线性回归方程有意义
• 计算检验统计量 F：
  • H₀ 成立时，$$ F = \frac{\frac{ESS}{1}}{\frac{RSS}{n-2}} = \frac{MSR}{MSE} \sim F(1, n-2) $$
  • 若 F > F_1-a (1, n-2)，拒绝 H₀，否则接受 H₀

回归系数检验

• 回归系数显著性检验的目的是通过检验回归系数 β 的值与 0 是否有显著性差异，来判断 Y 与 X 之间是否有显著的线性关系，若 β=0，则总体回归方程中不含 X 项 (即 Y 不随 X 变动而变动)，因此，变量 Y 与 X 之间并不存在线性关系；若 β ≠ 0，说明变量与 X 之间存在显著性的线性关系
• 

线性关系检验与回归系数检验的区别

• 线性关系的检验是检验自变量与因变量是否可以用线性来表达，而回归系数的检验是对样本数据计算的回归系数检验是否为 0
• 在一元线性回归中，自变量只有一个，线性关系检验与回归系数检验是等价的
• 在多元回归分析中，这两种检验的意义是不同的。线性关系检验只能用来检验总体回归关系的显著性，而回归系数检验可以对各个回归系数分别进行检验

估计和预测

• 点估计：利用估计的回归方程，对于 x 的某一个特定的值，求出 y 的一个估计值就是点估计
• 区间估计：利用估计的回归方程，对于 x 的一个特定值，求出 y 的一个估计值的区间就是区间估计

估计标准误差

• 为了度量回归方程的可靠性，通常计算估计标准误差度量观察值回绕着回归直线的变化程度或分散程度
• 估计标准误差越大，则数据点围绕回归直线的分散程度就越大，回归方程代表性就越小
• 估计标准误差越小，则数据点围绕回归直线的分散程度越小，回归方程的代表性越大，可靠性越高

• y 是给的样本，y^ 是估计的方程上的点，就是 x 同下的 y^，这也是残差平方和，分子
• 分母是样本数量 - 变量数量

置信/预测区间估计

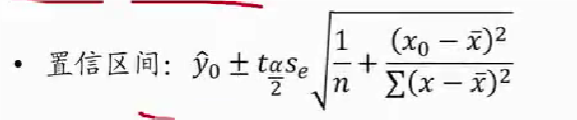
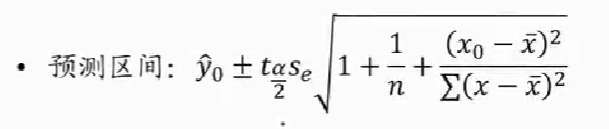
非线性回归

• 首先根据数据画出图像，也就是散点图，然后根据散点图大致推测是什么类型曲线，指数型，x².....
• 根据这个曲线，转换为线性回归形式，利用线性回归求得系数
• 比如下面的倒指数形式的，转换为 y' = a' + bx' 后，y' 可以根据 y 算出，然后后面同理，就能根据一元线性回归的方程计算出系数 a', b'，就能算出原方程形式

双曲线

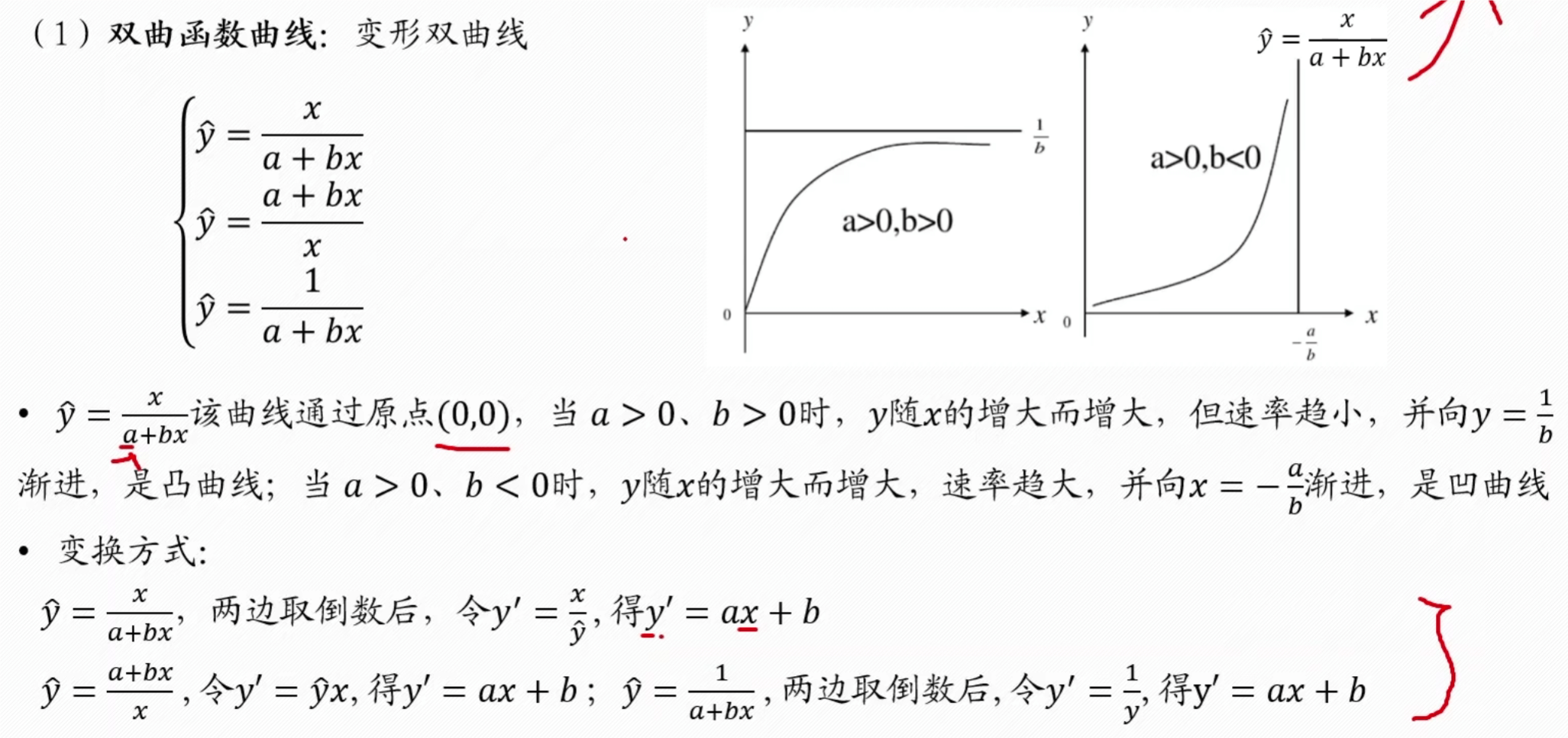
幂函数

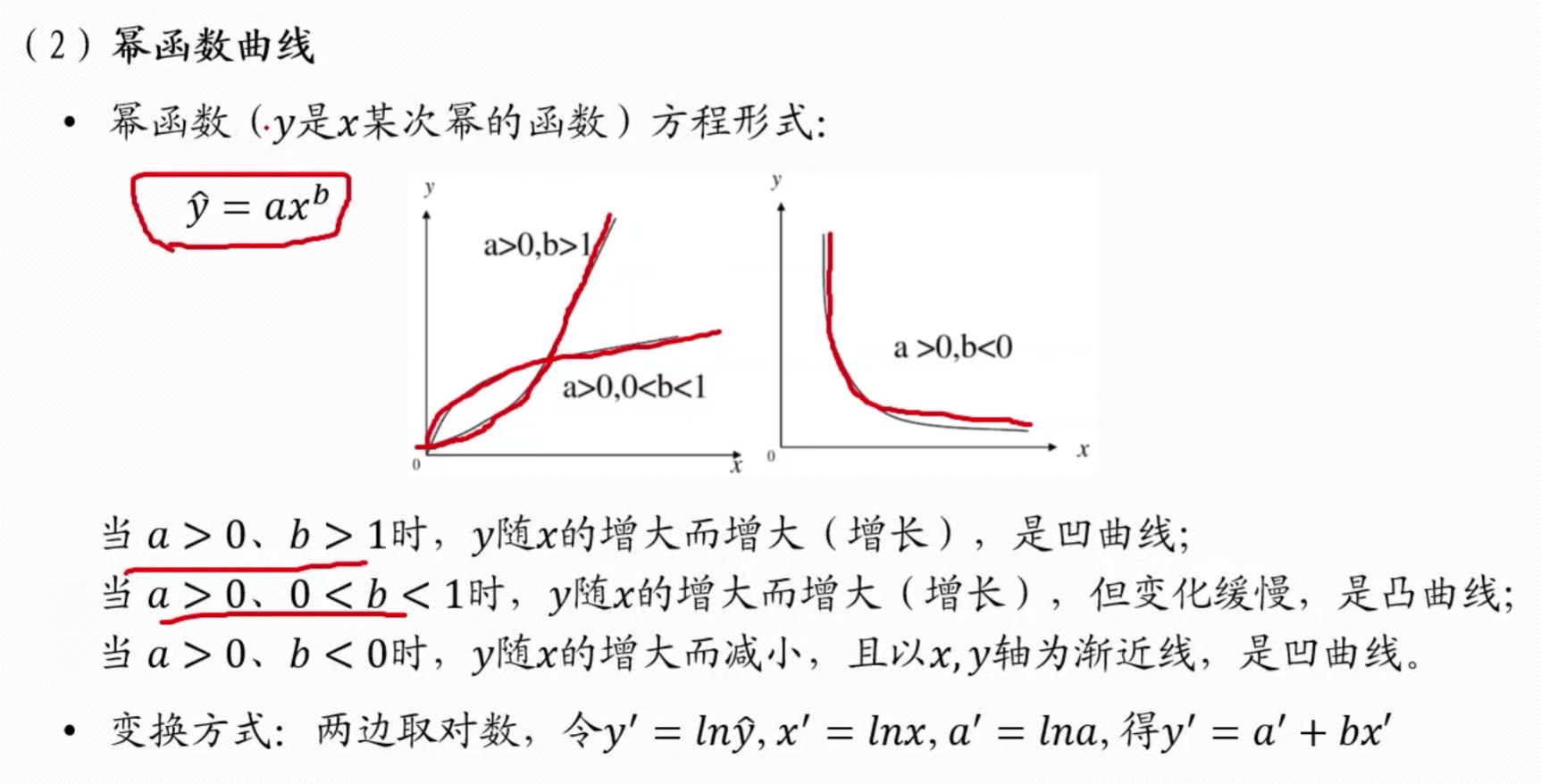
指数

倒指数

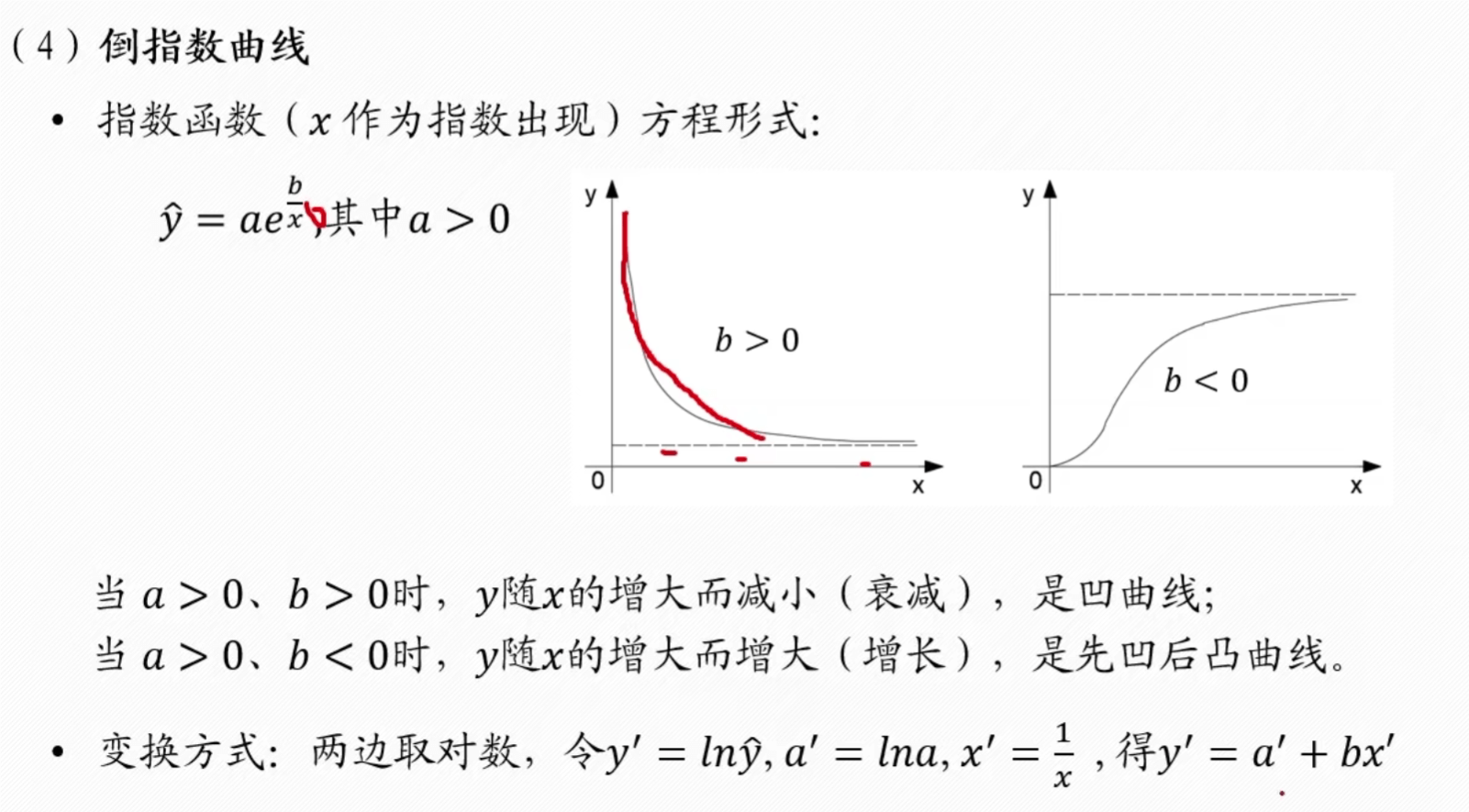
对数

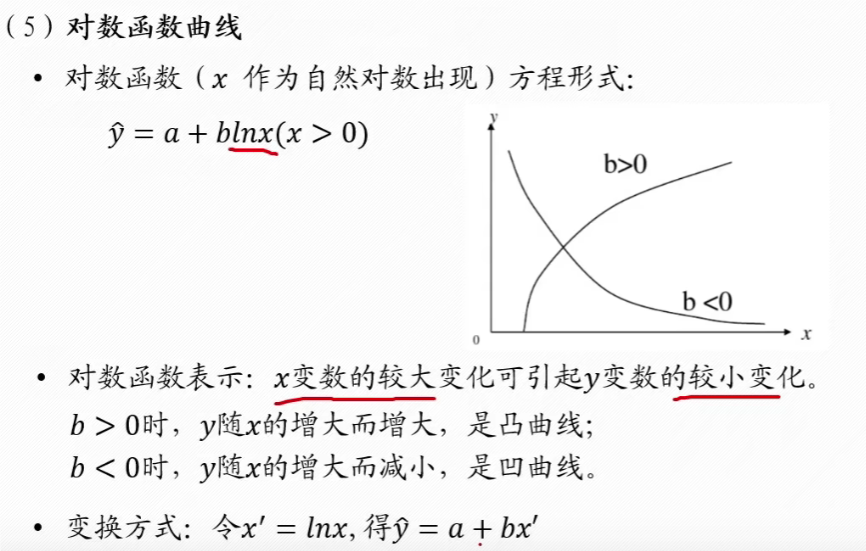
S 型曲线

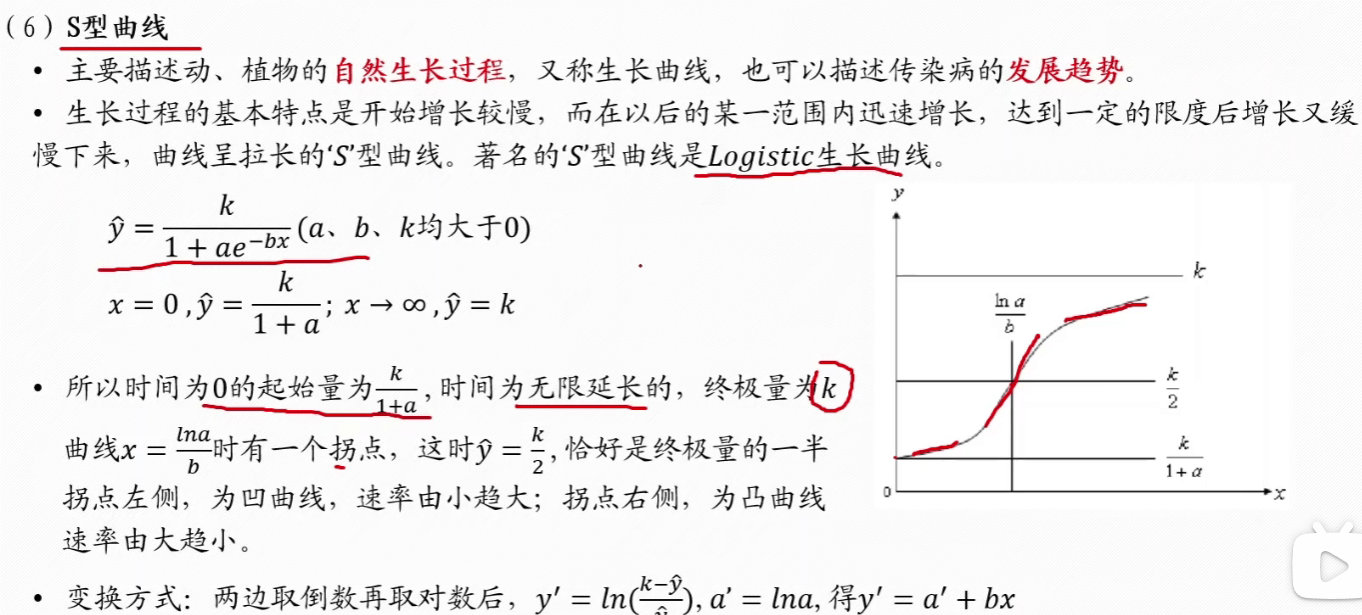
如果曲线都不是上述的，使用一般方法

灰色预测 GM (1, 1)

• 所谓灰色预测，就是对既含有已知信息又含有不确定信息的系统进行预测，就是对在一定围内变化的、与时间有关的灰色过程进行预测

适用：

• 数据是以年份度量的非负数据 (如果是月份或者季度数据一般要用时间序列模型)，比如定时求量的题目，即已知一些年份数据，预测下一年的数据，常见有 GDP、人口数量、耕地面积、粮食产量等；或者定量求时，已知一些年份数据和某灾变的阈值，预测下次灾变时间
• 数据能经过准指数规律的检验 (除前两期外，后面至少 90%的期数的光滑比要低于0.5)
• 数据的期数较短且和其他数据之间的关联性不强 (小于等于 10，数据的期数较短且和其他数据之间的也不能太短了，比如只有 3 期数据)，要是数据期数较长，一般用传统的时间序列模型比较合适

总体思路：

• 根据原始的离散非负数据列，通过累加等方式削弱随机性、获得有规律的离散数据列
• 建立相应的微分方程模型，得到离散点处的解
• 再通过累减求得的原始数据的估计值，从而对原始数据预测

步骤：

• 将数据描图，发现没有规律

• 若新曲线想指数曲线，那么利用指数曲线的表达式逼近 x⁽¹⁾

• 构建一阶常微分方程，求解拟合指数曲线的函数表达式 $$ \frac{dx^{(1)}}{dt} + ax^{(1)} = u $$

• 为了求解 x⁽¹⁾，求解出 a 和 u

• 

• 

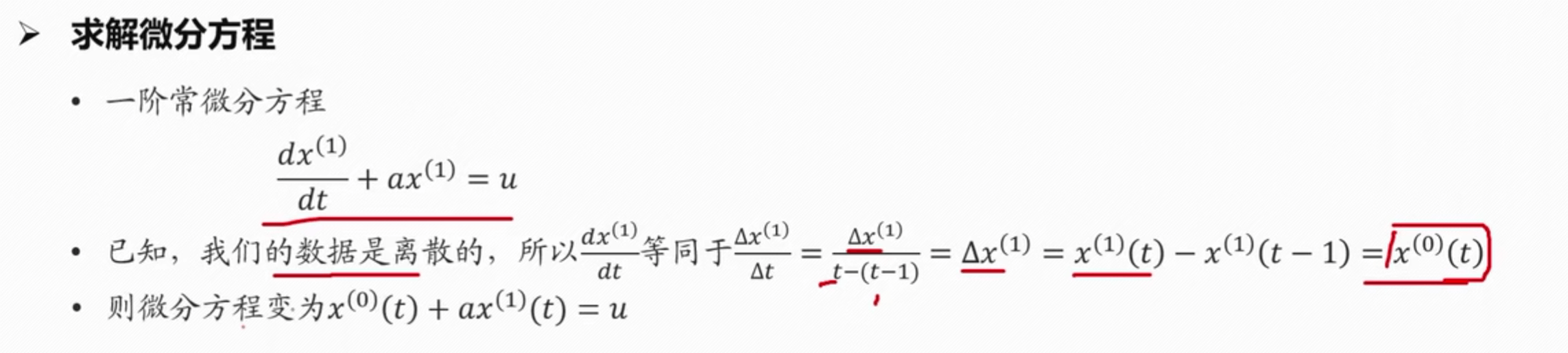
• 利用线性规划或者最小二乘法求解，因为 x⁽⁰⁾ 和 z^{(1 )}已知

• 检验

• 对原始数据检验，判断是否可以用灰色预测模型，进行级比检验

• 

• 检验模型对原始数据的拟合程度

• 

时间序列模型（ARIMA）

几种模型

白噪声是指误差的随机选择

ARIMA 模型的建模步骤：

• 对序列绘图，进行平稳性检验，观察序列是否平稳; 对于非平稳时间序列要先进行 d 阶差分，转化为平稳时间序列;
• 经过第一步处理，已经得到平稳时间序列。要对平稳时间序列分别求得其自相关系数 (ACF)和偏自相关系数 (PACF)，通过对自相关图和偏自相关图的分析或通过 AIC/BIC 搜索，得到最佳的阶数 p、q;
• 由以上得到的 d、q、p，得到 ARIMA 模型。然后开始对得到的模型进行模型检验

平稳性

• 平稳性就是要求经由样本时间序列所得到的拟合曲线在未来的一段时间内仍然能够按照现有的形态延续下去
• 平稳性要求序列的均值和方差不发生明显变化
  • 严平稳：序列所有的统计性质（期望，方差）都不会随着时间的推移而发生变化
  • 宽平稳：期望与相关系数（依赖性）不变，就是说 t 时刻的值 X 依赖于过去的信息
• 实际数据大致上都是宽平稳
• 如果一个时间序列不是平稳的，通常需要通过差分的方式将其转化为平稳时间序列

画图看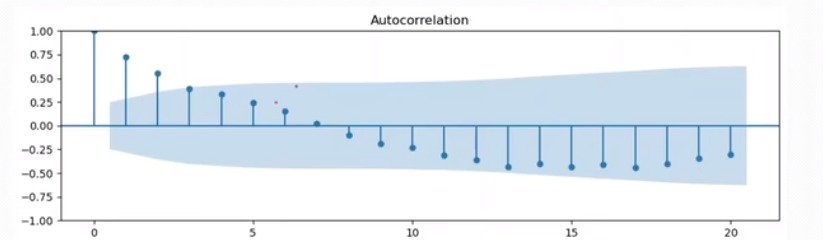， 蓝色部分为置信区间，发现几乎都位于置信区间之中，说明训练集就是一个平稳序列，不需要差分了

==差分法实现==

• 时间序列在 t 和 t-1 时刻的差值 $$\Delta yx = y(x + 1) - y(x),(x = 0,1,2,...) $$

• 一般差分次数不易过多，最高2、3 次即可

自相关系数 （ACF）与偏自相关系数（PACF)

ADF 检验

• 判断是否是平稳序列的一个计算方法
• ADF 检验就是判断序列是否存在单位根：如果序列平稳，就不存在单位根；否则，就会存在单位根

import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
import pandas as pd

# 数据一、随机数据
# data = np.random.randint(6, 10, 300)

# 数据二、待测数据
data = pd.read_csv("filename.xlsx", usecols=[1]).values

plt.plot(data)

alpha = 0.05
result = adfuller(data)
print((result))
if result[1] < alpha:  # p_value值大，无法拒接原假设,有可能单位根，需要T检验
    print("stationarity")
else:
    if result[0] < result[4]['5%']:  # 代表t检验的值小于5%,置信度为95%以上，这里还有'1%'和'10%'
        print("stationarity")  # 拒接原假设，无单位根，平稳的
    else:
        print("no_stationarity")  # 无法拒绝原假设，有单位根，不平稳的


"""
第一个是adt检验的结果，简称为T值，表示t统计量。
第二个简称为p值，表示t统计量对应的概率值。
第三个表示延迟。
第四个表示测试的次数。
第五个是配合第一个一起看的，是在99%，95%，90%置信区间下的临界的ADF检验的值。
 
第一点，1%、%5、%10不同程度拒绝原假设的统计值和ADF Test result的比较，
ADF Test result（第一个值）同时小于1%、5%、10%即说明非常好地拒绝该假设。本数据中，adf结果为-8， 小于三个level的统计值
第二点，p值要求小于给定的显著水平，p值要小于0.05，等于0是最好的。本数据中，P-value 为 1e-15,接近0.
p值为0.0229<0.05，说明在5%下显著，即拒绝原假设，是平稳的
"""

拖尾和截尾

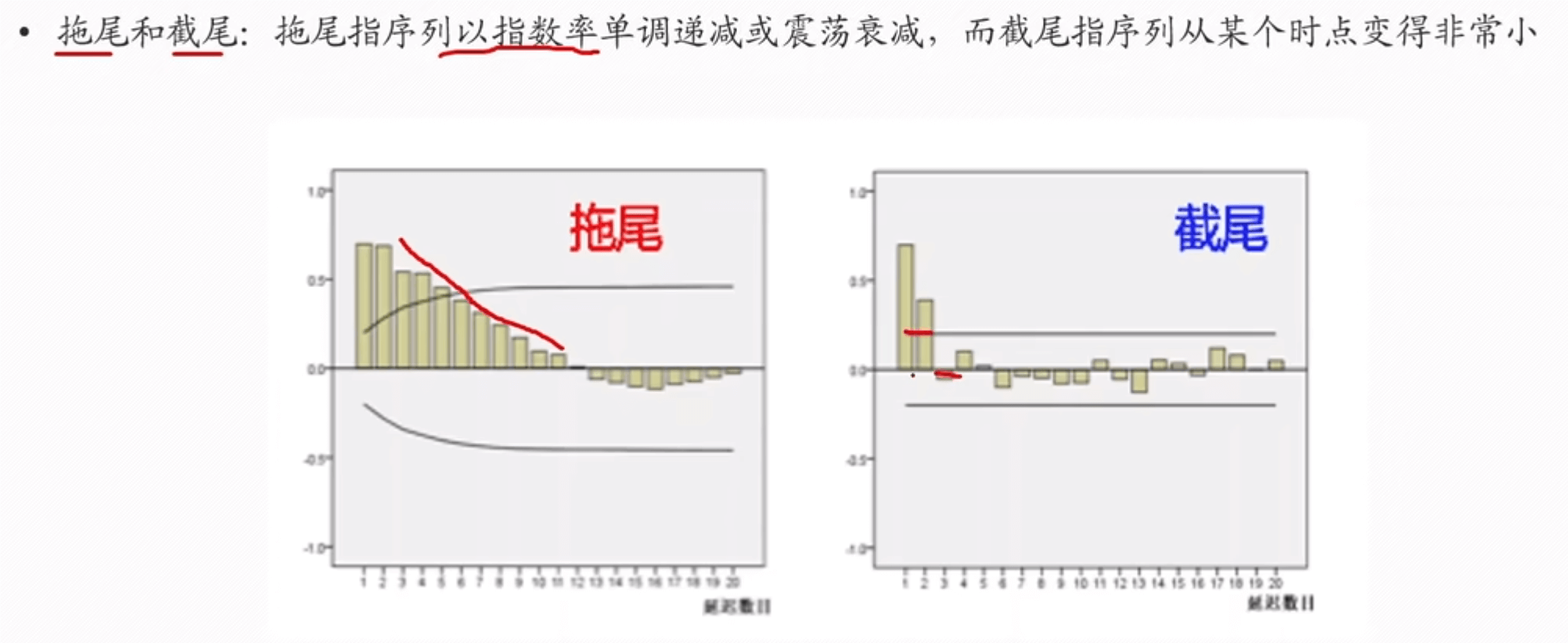
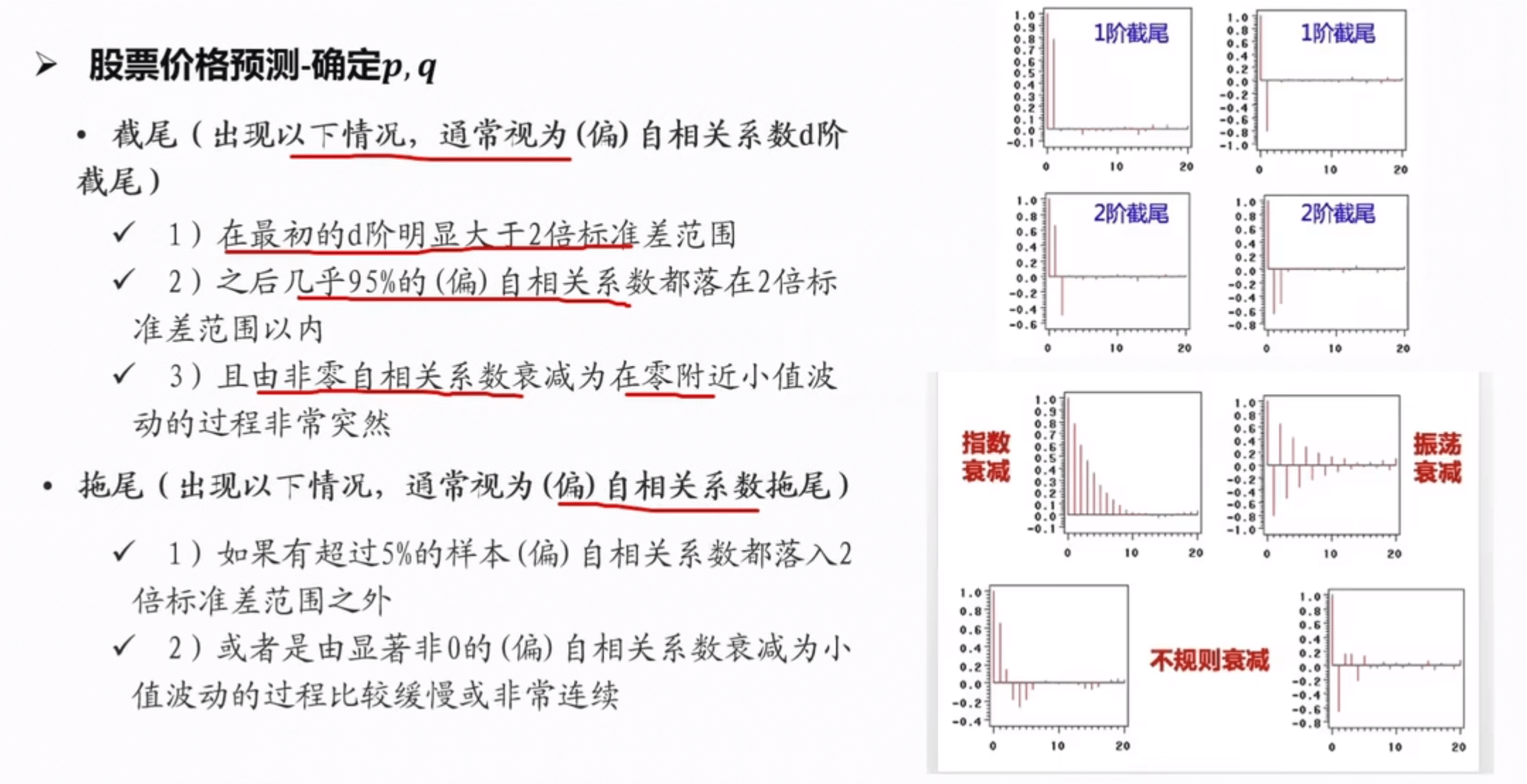
==确定 p，q 值==

d 的值为差分的次数

法一：

法二：BIC 和 AIC 准则

# BIC准则
results_bic.stack().idxmin() # 结果为 'AR1','MA0'，说明p为1，q为0

# AIC 准则和 BIC 准则对训练数据 train 进行选择
# 目前理解是 train 是进行差分后的平稳序列
train_results = sm.tsa.arma_order_select_ic(train,ic=['aic', 'bic'],trend='n',max_ar=8,max_ma=8)
print('AIC',train_results.aic_min_order)
print('BIC',train_results.bic_min_order)
# 结果为 AIC(2, 1)  BIC(1, 0)  ---> (p,q)
# 这里限制了自回归项(AR)和移动平均项(MA)的最大阶数，将其设置为 8
# BIC 更好

==模型检验==

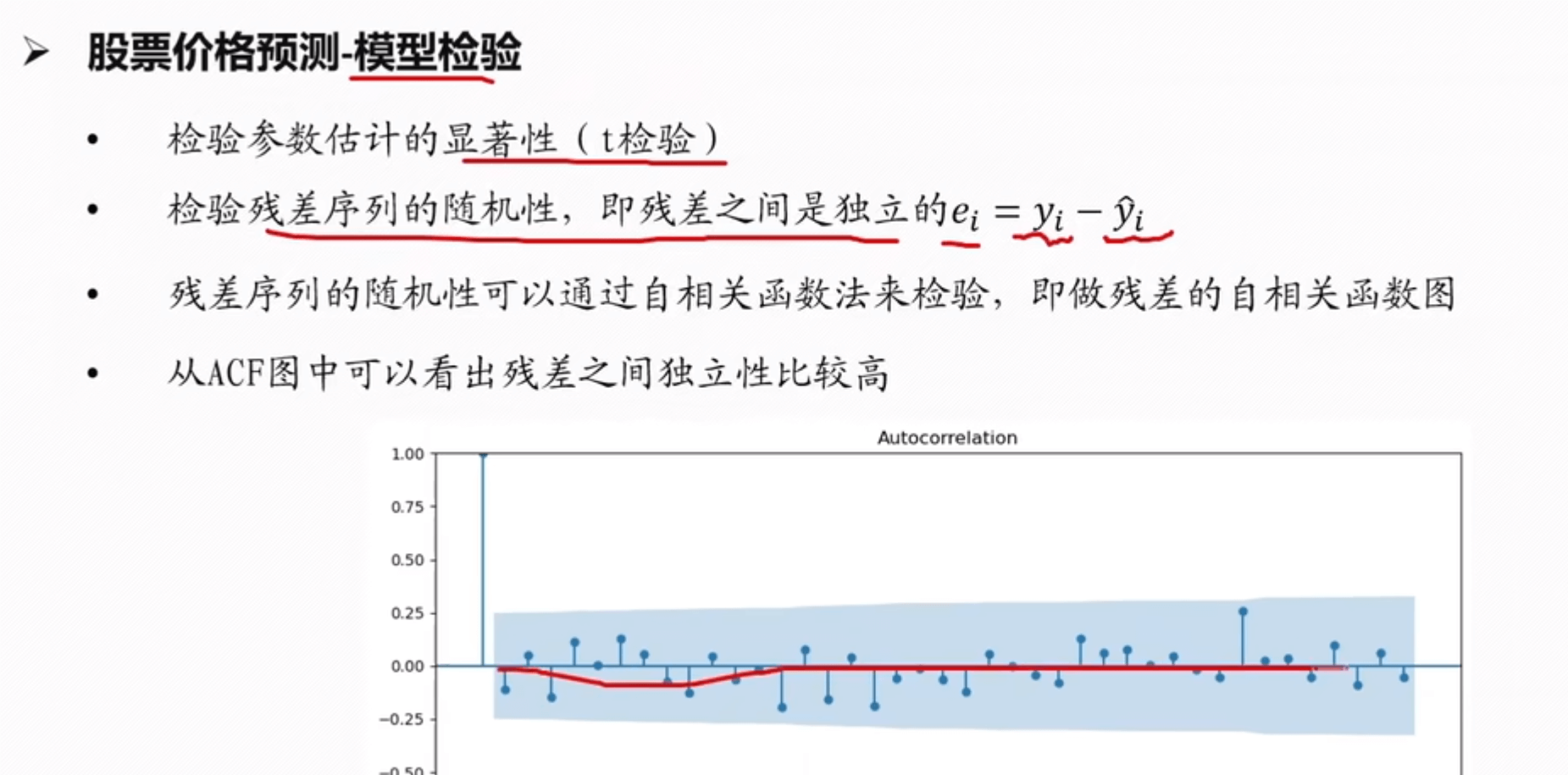
示例部分

代码 copy: 【Python数学建模常用算法代码（一）之ARIMA时间序列预测模型】_arimapython代码-CSDN博客

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

# 读取时间序列数据
data = pd.read_csv('time_series_data.csv', index_col='Date', parse_dates=True)
ts = data['Value']

# 绘制时间序列图
plt.plot(ts)
plt.title('Time Series Data')
plt.show()

# 检验平稳性
result = adfuller(ts)
print('ADF Statistic:', result[0])
print('p-value:', result[1])

# 如果数据非平稳，进行差分处理
if result[1] > 0.05:
    ts_diff = ts.diff().dropna()

# 绘制 ACF 和 PACF 图
plot_acf(ts_diff)
plot_pacf(ts_diff)
plt.show()

# 构建 ARIMA 模型
p = 1  # 根据 PACF 图选择
d = 1  # 差分一次
q = 1  # 根据 ACF 图选择

model = ARIMA(ts, order=(p, d, q))
model_fit = model.fit()

# 打印模型摘要
print(model_fit.summary())

# 进行预测
forecast = model_fit.forecast(steps=10)
print(forecast)

---

说明：是在 https://www.bilibili.com/video/BV1EK41187QF 学习后的总结，方便记录，截屏许多公式